Les méthodes de réglage
Réglage par approches successives ou méthode du régleur
Cette méthode n'est valable que pour un procédé naturellement stable en boucle ouverte. Elle s'applique en boucle fermée.
La méthode par approche successives consiste à modifier les actions du régulateur et à observer les effets de ces modifications sur la mesure, jusqu'à obtenir la réponse optimale. Cette méthode est couramment utilisée dans l'industrie de par la simplicité de sa mise en œuvre.
On se place tout d'abord en mode manuel pour stabiliser la mesure au point de consigne ce qui permet de passer en mode automatique sans à coups. De petites variations sur la consigne permettent d'observer les réactions naturelles du procédé afin de dégrossir les actions à mettre sur le régulateur au début de chaque réglage par approches successives.
Les actions sont réglées dans l'ordre P, D, I et on considère toujours les trois critères principaux permettant d’apprécier les performances d’une régulation :
- La précision : évaluée par l'écart statique
- La rapidité : évaluée par le temps de réponse
- La stabilité : évaluée par le premier dépassement
Réglage de Ziegler-Nichols
Cette méthode est basée sur la recherche des oscillations juste entretenues = pompage du système en boucle fermée.
- Le système est en régulation proportionnelle (actions intégrale et dérivée annulées). On diminue la bande proportionnelle jusqu’à obtenir un système en début d’instabilité, le signal de mesure M et la sortie du régulateur YR sont périodiques, sans saturation.
- On relève alors la valeur du gain proportionnel critique Ac ainsi que la période des oscillations Tc correspondants.
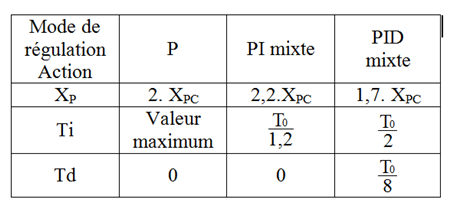
- La mesure de la période des oscillations TC et du gain critique Ac permet de calculer les actions PID du régulateur.
Réglage de Broïda
Il suffit d’effectuer en manuel un échelon de signal de commande Yr et d’observer la mesure M. Si on obtient une courbe en S on peut modéliser le système en BO par le modèle de Broïda.
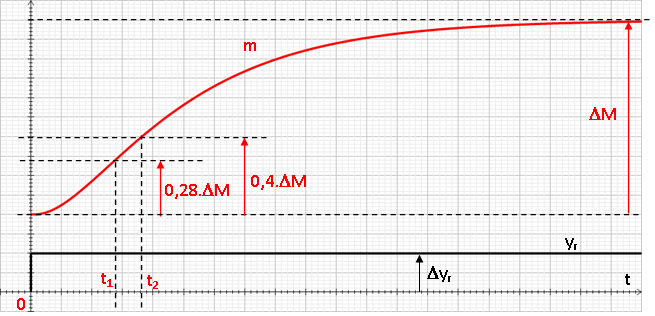
On obtient donc une FTBO de la forme
\[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{K\times e^{-Tp}}{1+\tau p}}\]
Pour calculer les paramètres:
\(T=2,8t1-1,8t2\)
et
\(\tau=5,5(t2-t1)\)
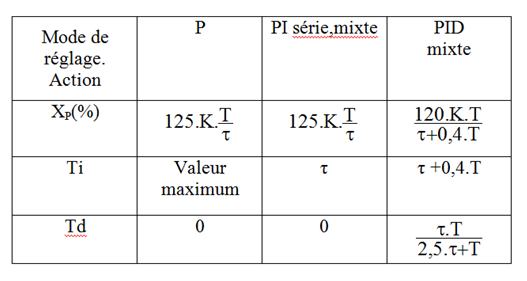
Cette méthode est fondée sur l’obtention de marges de stabilité fixées : marge de gain de 6dB et marge de phase de 45°.
Elle permet d’obtenir le tableau de réglage suivant :