Systèmes du premier ordre
Définition
Un système est dit du premier ordre si la relation liant la variation de m(t) à la variation de yr(t) qui lui a donné naissance peut se mettre sous la forme d'une équation différentielle du premier ordre: \[\boxed{\tau \dfrac{dm(t)}{dt}+m(t)=K yr(t)}\] où:
- K:gain statique du système
- \(\tau\):constante de temps du système (s)
Exemple de système du 1er ordre: Chauffage d'une enceinte
On maintient la température d'une enceinte constante par action sur une résistance chauffante de puissance maximale \(P_{max}\). Les pertes d'énergie sont proportionnelles à la différence de température entre l'enceinte et le milieu ambiant \(\theta -\theta_{ambiant}\).
Le coefficient de proportionnalité est noté h. L'enceinte est assimilée à un corps de capacité thermique C.
Le schéma bloc du système peut se mettre sous la forme suivante :

étude du système
Nous réalisons un bilan thermique sur l'enceinte. \((energie reçue) - (energie perdue)= (variation d'energie de l'enceinte)\) soit une fois mis en équation: \[P\Delta t - h(\theta -\theta_{ambiant})\Delta t = C\Delta \theta\] Qui sous forme dérivée peut se mettre sous la forme:\[P - h(\theta -\theta_{ambiant}) = C\dfrac{d\theta}{dt} \] D'autre part, la puissance de chauffe est proportionnelle au signal de commande, d'où: \( P=\dfrac{yr(t)}{100} \times P_{max}$\) et le signal de mesure fourni par le transmetteur est proportionnel à la température (en supposant le réglage du zéro réalisé à 0C), soit : \(m(t)=Kt \times\theta\) Tout calculs étant faits, l'équation différentielle reliant le signal de mesure au signal de commande peut se mettre sous la forme: \[\boxed{\tau \dfrac{dm(t)}{dt}+m(t)=M_{0}+Kyr(t)}\] où :\(\tau\) est une "constante" assimilable à un temps telle que \(\tau=\dfrac{C}{h}\) K est une "constante" sans unités telle \(K=\dfrac{KtP_{max}}{100h}\) %Résolution de l'équation différentielle
Fonction de transfert d'un système du premier ordre
La fonction de transfert d'un système du premier ordre est de la forme: \[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{K}{1+\tau p}}\] où:
- K:gain statique du système
- \(\tau\):constante de temps du système (s)
Réponse indicielle des systèmes du premier ordre
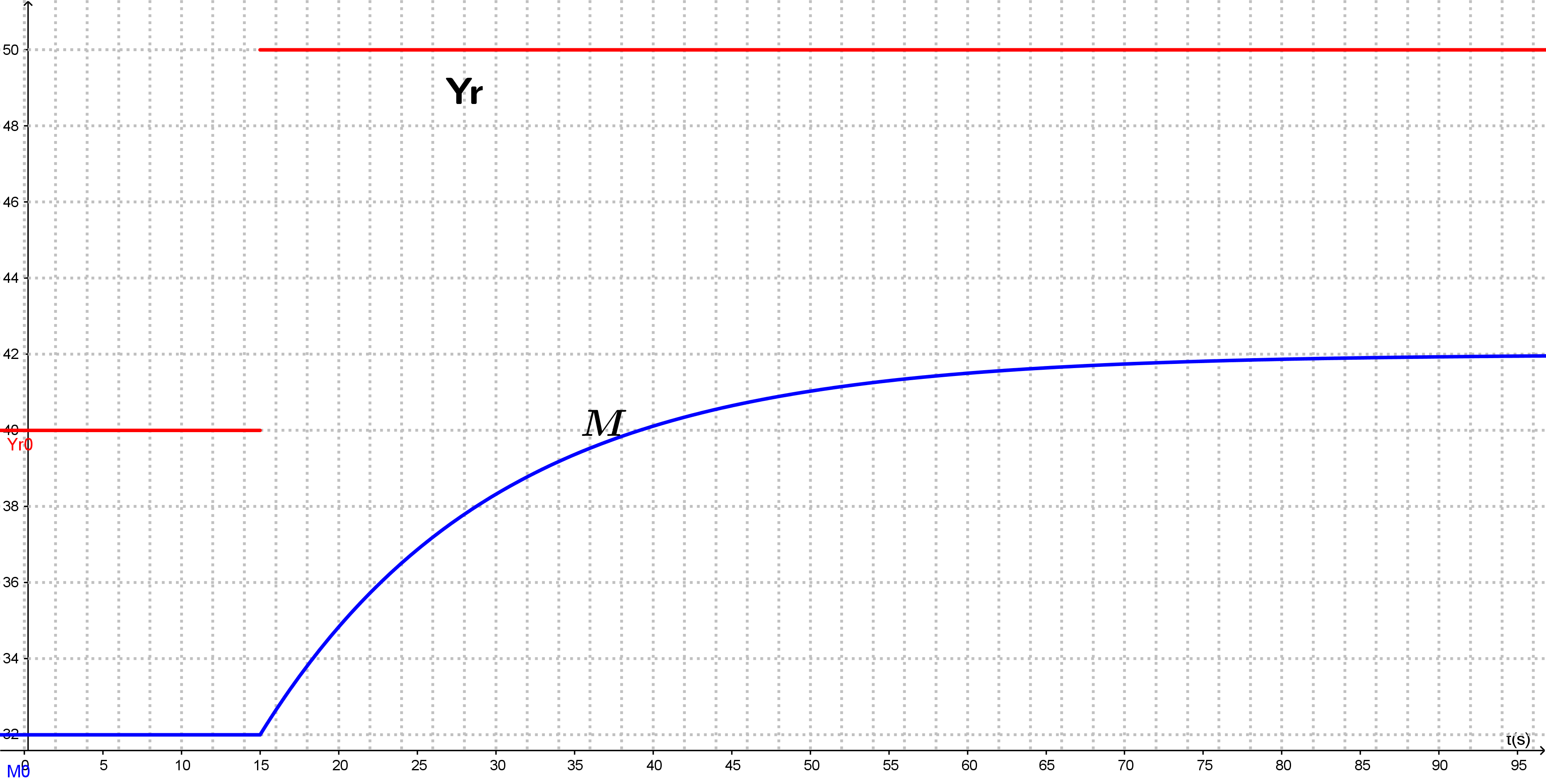
Réponse indicielle
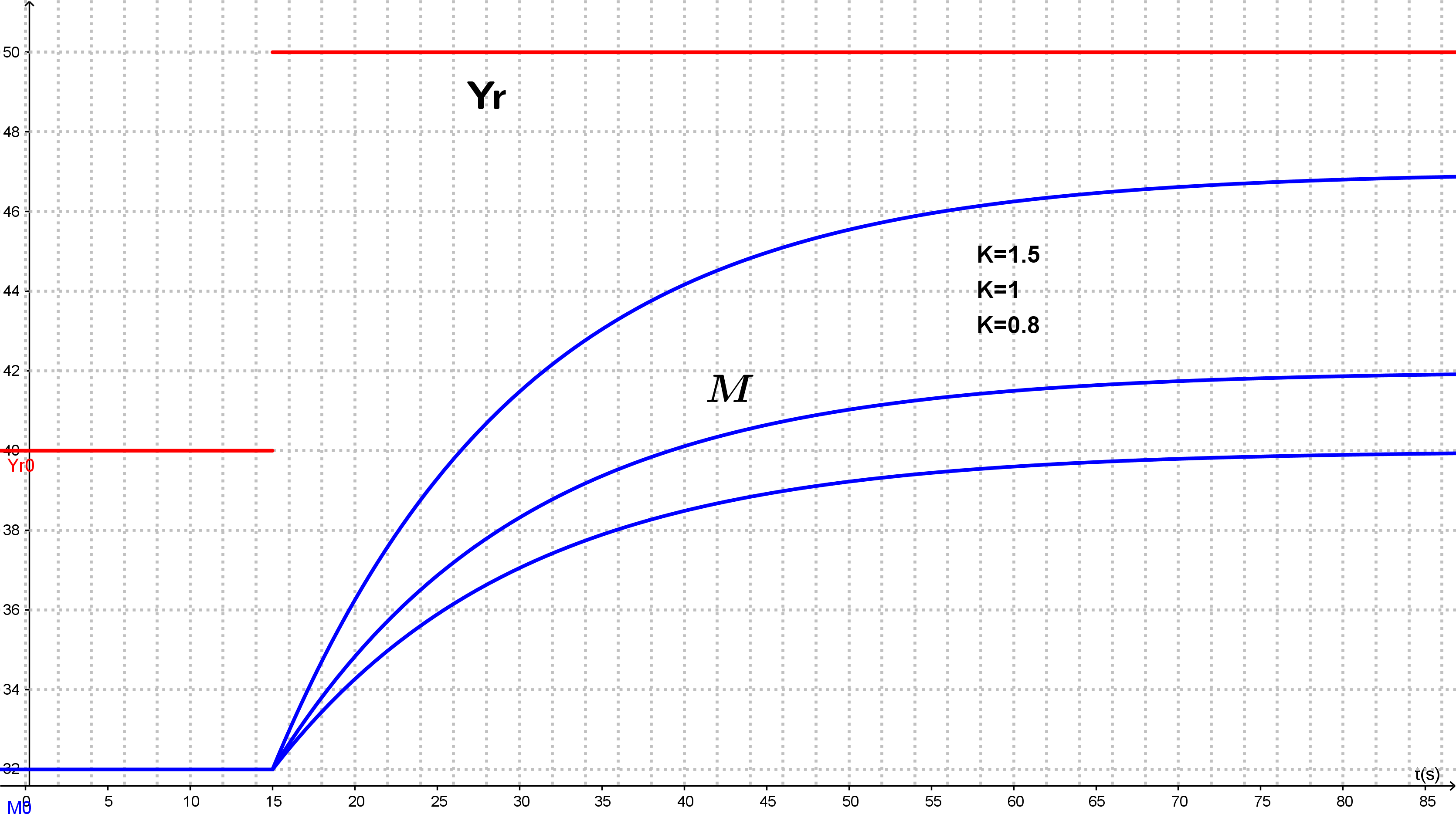
Influence du gain statique K
Le gain statique d'un système renseigne sur l'amplitude ses variations. Pour un même échelon de commande, un système évoluera d'autant plus en amplitude que son gain statique est élevé (en valeur absolue).
Le gain statique d'un système peut être positif. On parle de procédé direct (à sens direct).
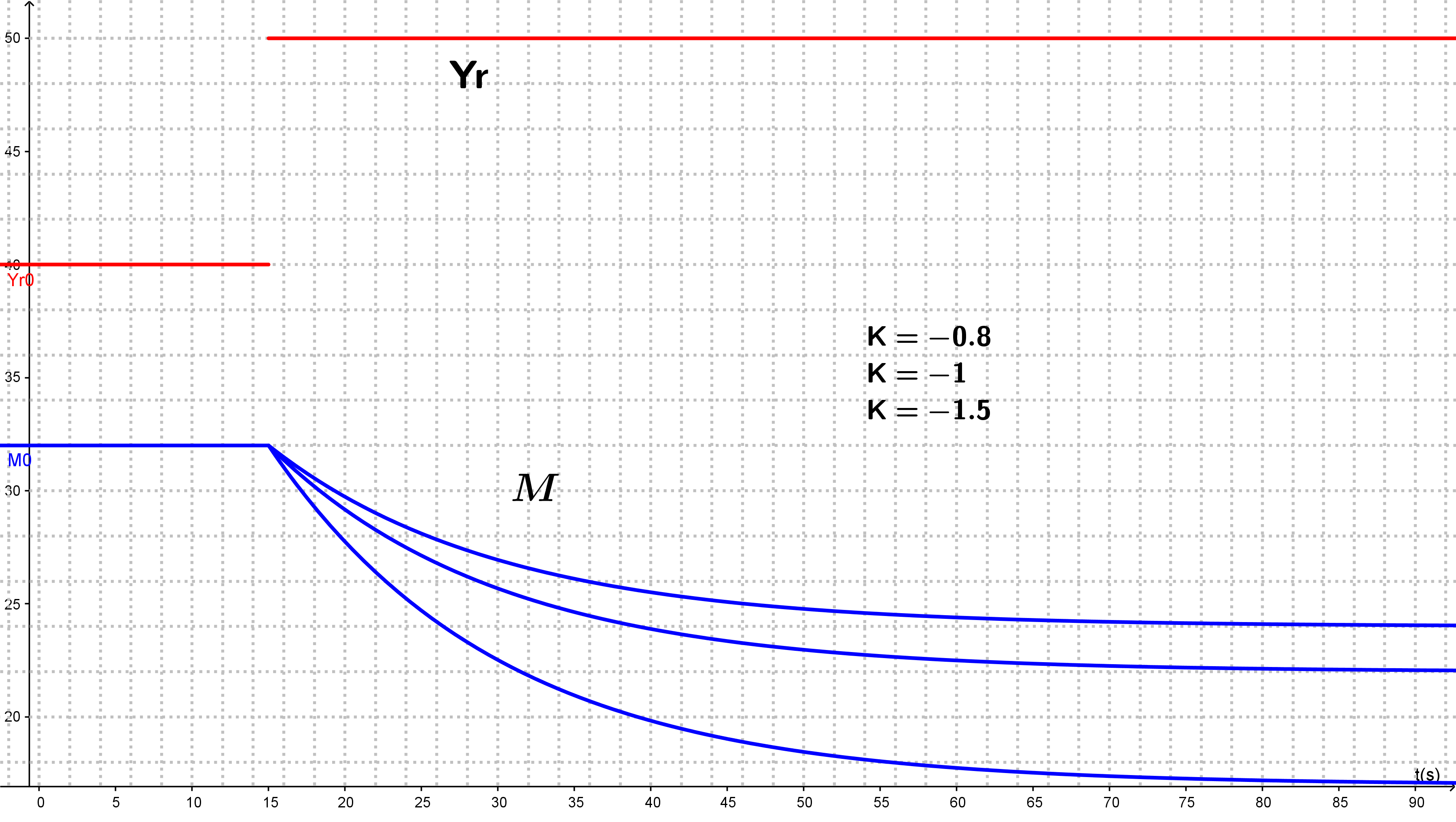
Le gain statique peut être négatif. on parle de procédé inverse (à sens inverse).
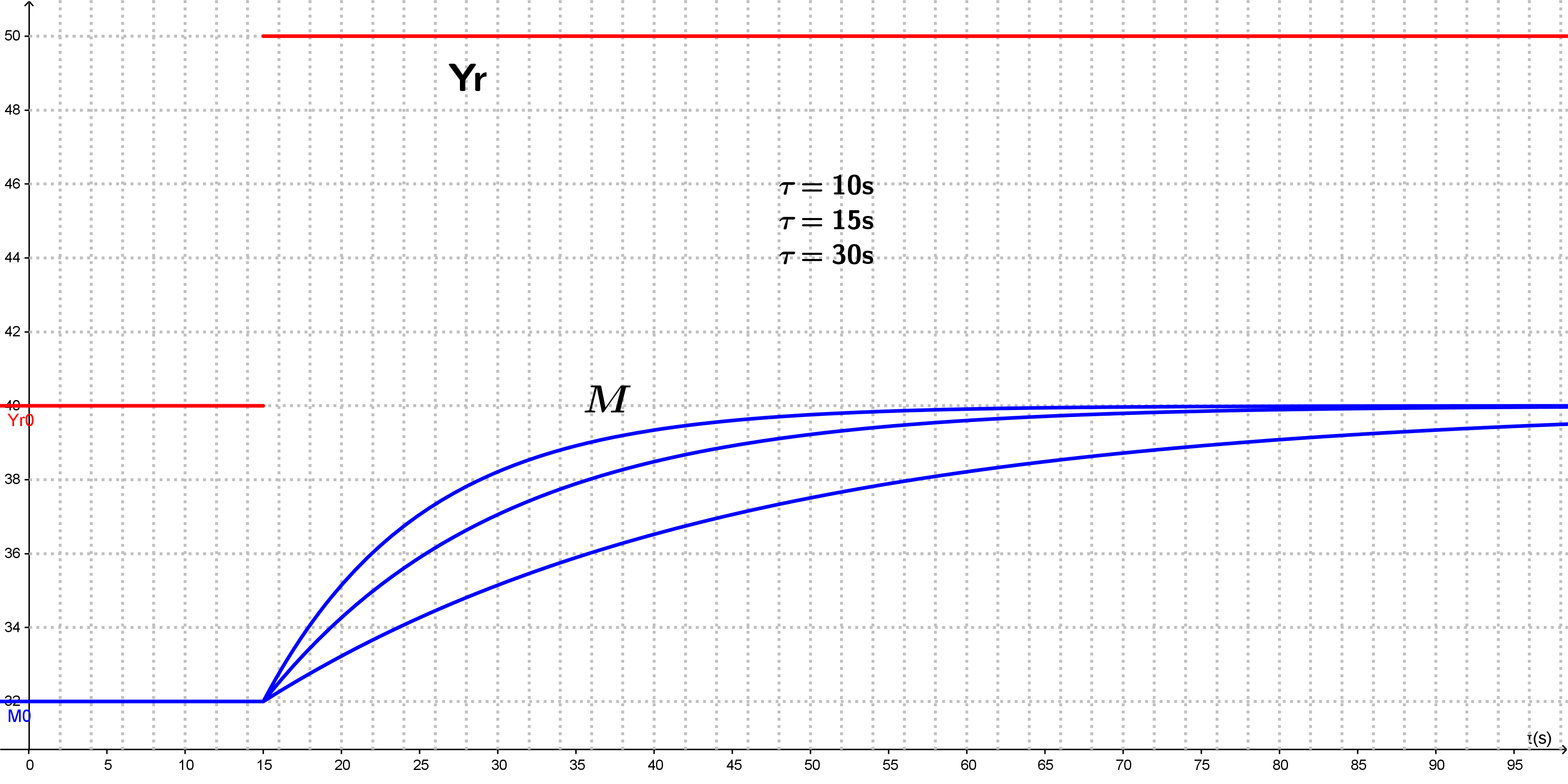
Influence de la constante de temps
La constante de temps d'un système renseigne sur son inertie. Plus la constante de temps est importante, et plus le système met du temps pour varier.
Influence du temps mort
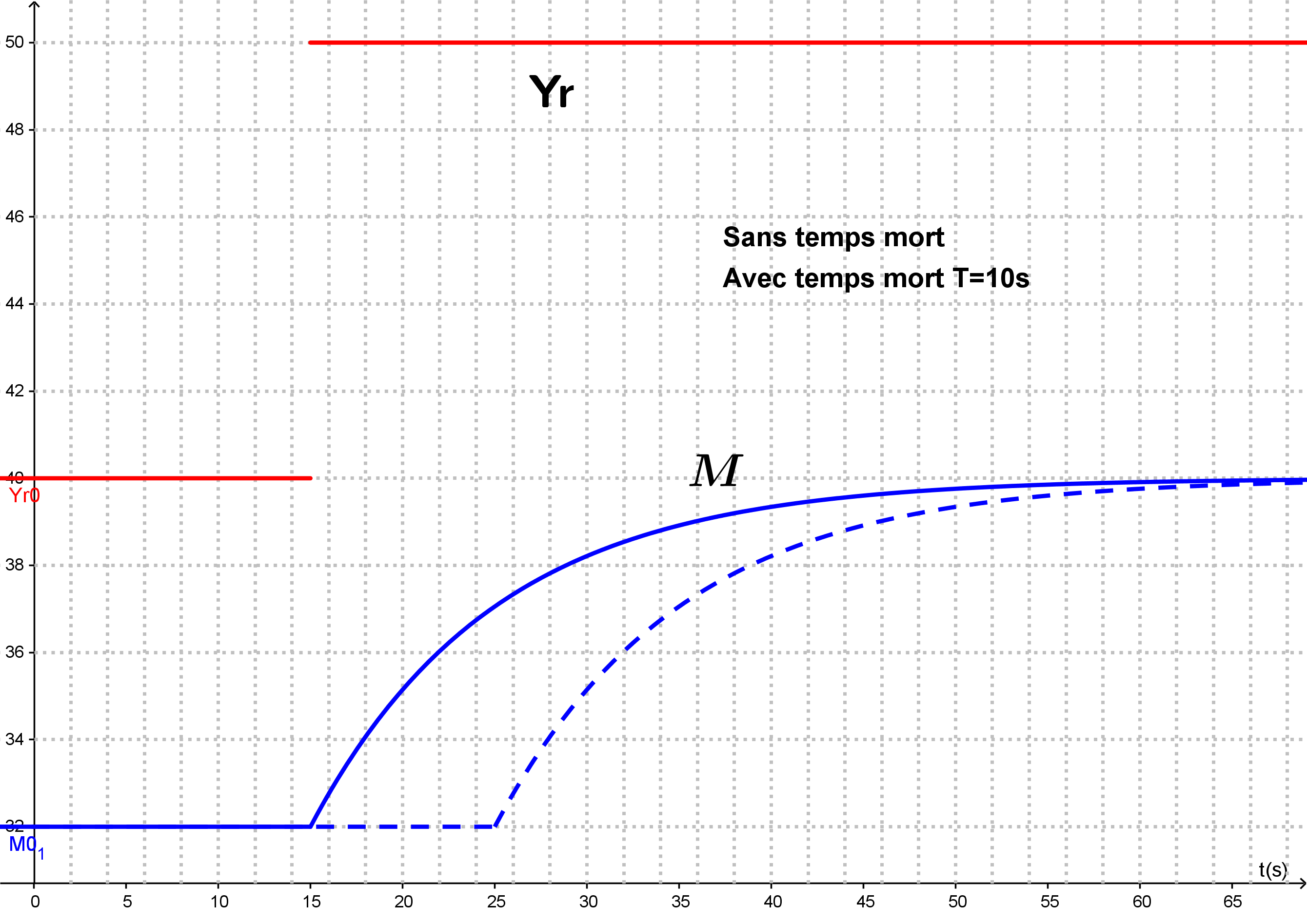
Un système peut présenter un décalage temporel entre l'instant où il est sollicité et l'instant où il se met à varier. Cette durée est appelée le temps mort, retard du système.
Modélisation des systèmes du premier ordre
Le gain statique est déterminé par: \[\boxed{K=\dfrac{\Delta M_{\infty}}{\Delta Yr_{\infty}}}\]
La constante de temps est estimé graphiquement comme étant la durée nécessaire pour que la mesure varie de 63% de sa variation totale. \[\boxed{\Delta M_{\tau}=0.63\Delta M_{\infty}}\]
Attention:
L'estimation de la constante de temps est réalisée à partir de l'instant où le système commence à varier.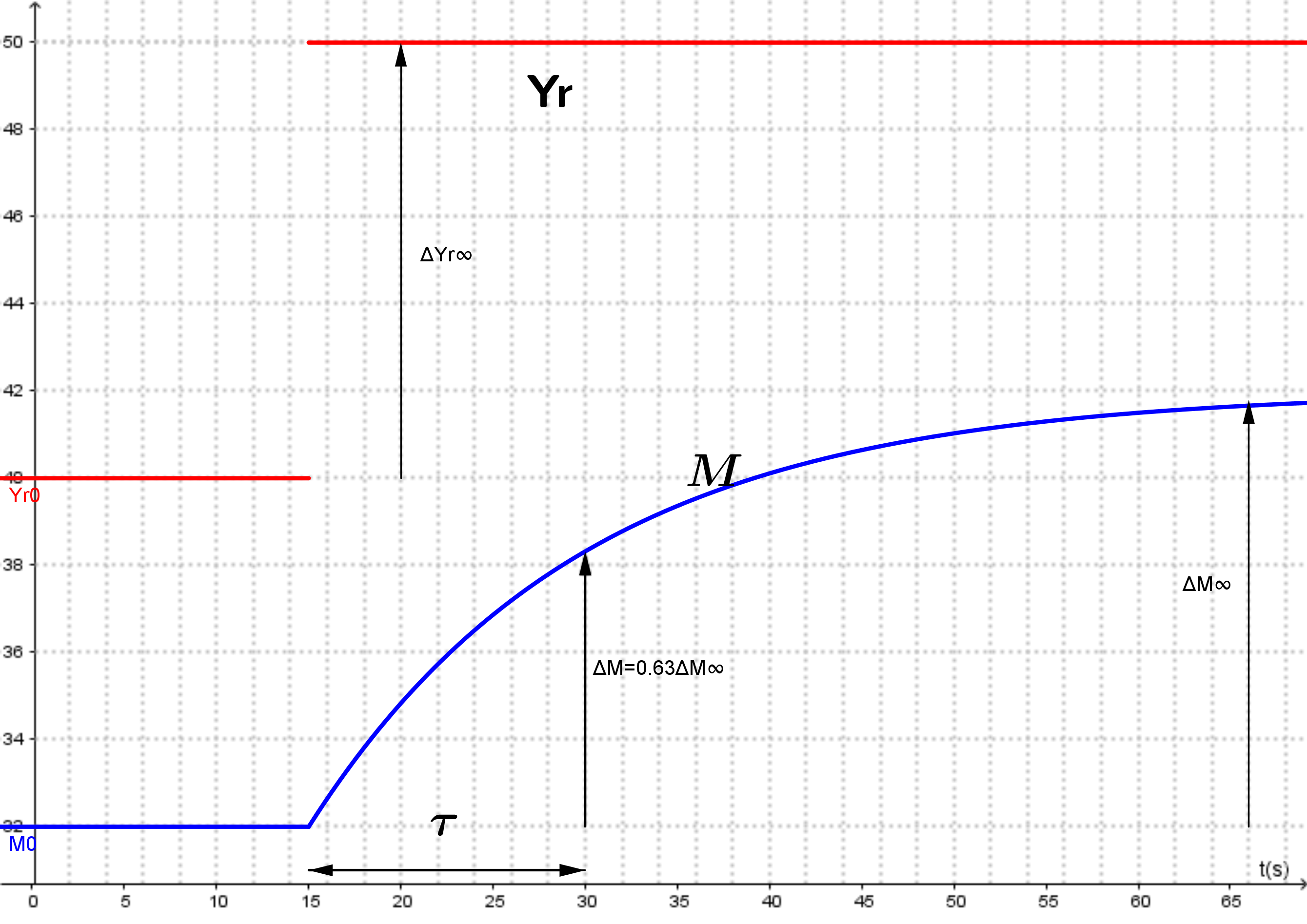
Systèmes à retard pur
Généralisation
Schéma Bloc
Équation temporelle
\[m(t)=K\times yr_{(t-T)}\]Fonction de transfert: \[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=Ke^{-Tp}}\]
D'où vient le temps mort
Aussi appelé retard, il est dû à un phénomène de- transport de matière
- transport d'énergie