Système intégrateur
Définition
Un système intégrateur est un système instable, c'est-à-dire qu'à partir d'un point de fonctionnement stable, une variation finie du signal de commande entraîne une variation infinie du signal de mesure.
C'est un système de classe 1 et d'ordre supérieur ou égal à 1.
Remarque: Un système est stable si à partir d'un point de fonctionnement stable, une variation finie du signal de commande entraîne une variation finie du signal de mesure.
Exemple de système
Remplissage d’une cuve dont le débit de vidange est constant. Le débit Qs en sortie de pompe volumétrique est constant.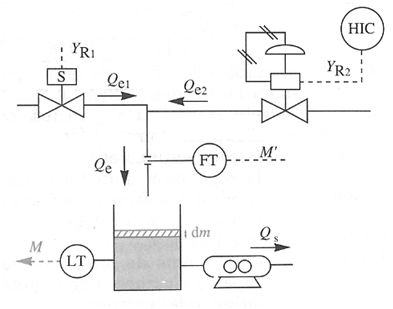
Au point de fonctionnement, Qs = Qe2.
L'électrovanne pilotant le débit Qe1 est une vanne tout ou rien.
Étude du système suite à l'ouverture de l électrovanne:On réalise un bilan matière sur la cuve, soit:\[Q_{e1}+Q_{e2}-Q_{s}=S\dfrac{dn(t)}{dt}\] or \(Q_{e2}(t)=Kv Yr_{2}(t)\) et \(m(t)=K_{t}n(t)\) d'où: \[\dfrac{dm(t)}{dt}=\dfrac{K_{t}K_{v}}{S}yr_{2}(t)\]qui peut se mettre sous la forme \[\dfrac{dm(t)}{dt}=k\times yr_{2}(t)\] On notera k : gain dynamique du système en \(s^{-1}\)
Réponse indicielle: La résolution de l'équation différentielle à un échelon d'amplitude \(\Delta Yr_{2}\) aboutit à la solution\[m(t)=m_{t_{0}}+k \Delta Yr_{2}\times (t-t_{0})\]avec \(m_{t_{0}}\) la valeur du signal de mesure à l'instant de l'ouverture de l'électrovanne \(t_{0}\)
Remarque :Le raisonnement et le résultat seraient identiques en considérant \(Yr_{1}\) variant entre 0 et 100%.
Fonction de transfert
Intégrateur pur:
\[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{k}{p}}\] avec k: gain dynamique du système en \(s^{-1}\)Il peut être associé à un système du 1er ordre ou autre, avec ou non temps mort.
En supposant que la vanne de régulation pilotée par Yr2 soit modélisable par un système du 1er ordre de constante de temps \(\tau_{2}\) , on obtient : \[H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{ke^{-Tp}}{p(1+\tau_{2}p)}\]
Modélisation
Sur les installations industrielles, il est possible de trouver des systèmes intégrateurs répondant aux fonctions de transfert suivantes.Modèle de Broïda
Il s'agit d'une méthode simple et rapide mais donnant un modèle grossier, mais suffisant dans la majorité des cas.
Elle permet d'écrire la fonction de transfert du procédé sous la forme d'un intégrateur pur retardé : \[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{ke^{-Tp}}{p}}\] avec : k : gain dynamique du procédé en \(s^{-1} ou min^{-1}\) T : temps mort du procédé en s ou min
On réalise, un relevé expérimental de la réponse indicielle du procédé à un échelon de commande de hauteur \(\Delta Yr\).
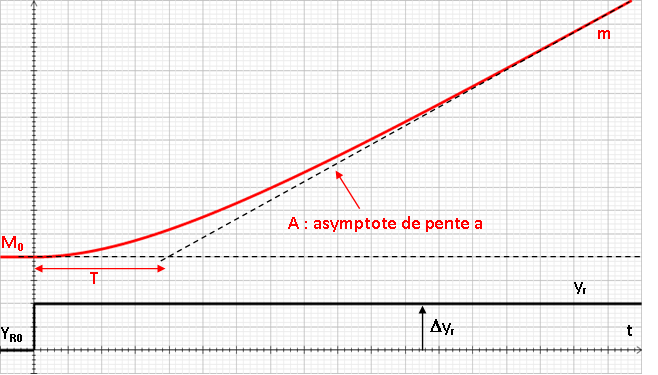
On trace l'asymptote A à la courbe de la mesure m, on mesure sa pente a ainsi que le temps mort T abscisse du point d'intersection entre l'asymptote A à m et l'axe horizontal correspondant à Mo.
On en déduit le gain dynamique : \(k=\dfrac{a}{\Delta yr}\) et la fonction de transfert H(p).
Modèle de Strejc
Cette méthode plus complexe, donne un modèle plus précis. Elle permet d'écrire la fonction de transfert du procédé sous la forme : \[\boxed{H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{k}{p(1+\tau p)^{n}}}\] avec : k : gain dynamique du procédé en \(s^{-1}\) ou\( min^{-1}\) \(\tau\) : constante de temps du procédé en s ou min n : ordre du système
On trace l'asymptote D1 à la courbe, sa parallèle D2 par A’, la parallèle A’A à l’axe des temps et le segment AC normal en A à A’A.
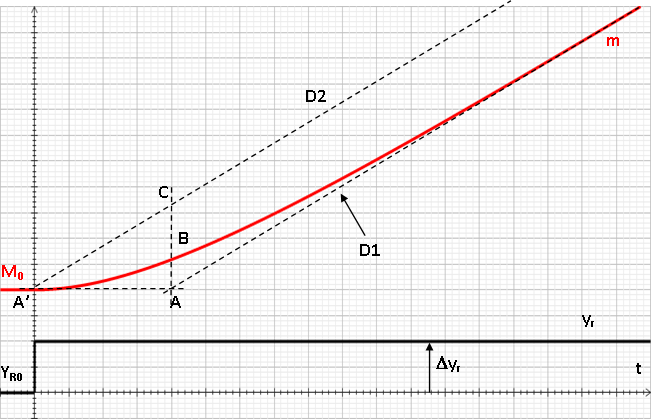
La pente a de la droite D1 permet de déterminer le gain dynamique \(k=\dfrac{a}{\Delta Yr}\)
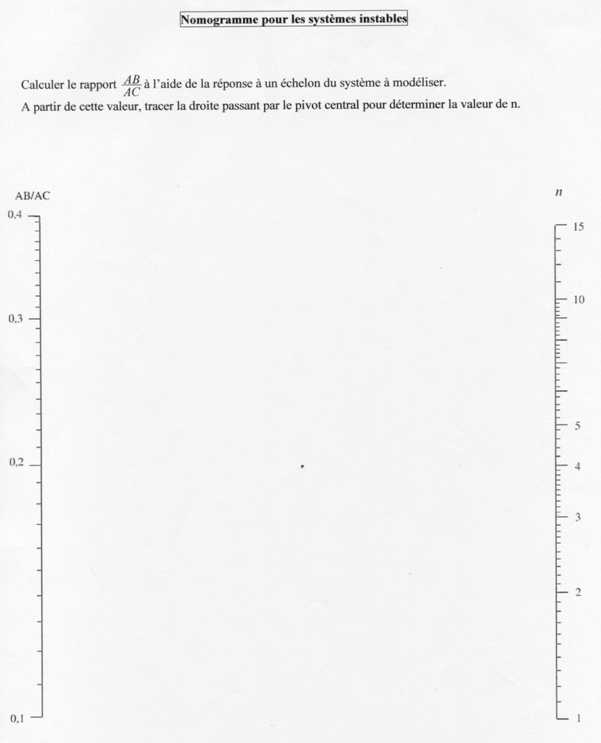
On calcule le rapport \(\dfrac{AB}{AC}\) . Ce rapport permet de déterminer n en utilisant le nomogramme puis \(\tau =\dfrac{A'A}{n}\); \(A’A\) étant exprimés en grandeur physique (s ou min, …).
Remarque
Parfois, on préfère avoir n entier, si n n'est pas entier alors on peut faire apparaître un temps mort en déterminant le nouveau rapport \(\dfrac{AB}{AC}\) correspondant à la partie entière de n.Pour cela déplacer D2 parallèlement à D1 pour obtenir ce nouveau rapport. Le temps mort T correspond alors à la translation effectuée par D2.