Le correcteur de Smith
Limite du régulateur PID sur les procédés à grand temps mort
On fournit ci-après la réponse à un échelon de consigne d'un système du premier ordre retardé \(H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{Ke^{-Tp}}{1+\tau p}=\dfrac{1.2e^{-3p}}{1+8p}\) en mode PI avec \(Ti=\tau\) et un gain de boucle \(AK=3\).
Suite à l'échelon de consigne, le régulateur augmente le signal de commande. La mesure ne commencera à varier qu'à partir d'une durée égale à la valeur du temps mort naturel.
Durant cette phase, l'action intégrale continue d'augmenter le signal de commande, pouvant entraîner sa saturation. Cette phase est préjudiciable à la stabilité du système.
Recherche d'un correcteur par modèle de référence
Le temps mort naturel du procédé ne peut être réduit. Ainsi il est illusoire d'obtenir une réponse en boucle fermée sans temps mort. Celui ci sera au minimum égal au temps mort naturel du procédé.
On se fixe donc comme comportement en boucle fermée: \[F(p)=\dfrac{M(p)}{W(p)}=\dfrac{e^{-Tp}}{1+\tau_{BF}p}\] avec :
- \(K_{BF}=1\): on souhaite une précision parfaite
- \(T\): temps mort naturel du procédé
- \(\tau_{BF}\): constante de temps du système en boucle fermée
Sachant que \(F(p)=\dfrac{M(p)}{W(p)}=\dfrac{C(p)H(p)}{1+C(p)H(p)}\), on montre que \[\boxed{C(p)=\dfrac{Yr(p)}{\epsilon(p)}=\dfrac{F(p)}{H(p)(1-F(p))}}\]
Tout calculs étant faits \[\boxed{C(p)=\dfrac{Yr(p)}{\epsilon (p)}=\dfrac{\tau}{K\tau_{BF}}(1+\dfrac{1}{\tau p})\left\{\dfrac{\tau_{BF}p}{1+\tau_{BF}p-e^{-Tp}}\right\}}\]
Réalisation pratique
Le correcteur est réalisé sous la forme d'un système bouclé:
Avec :
- \(B(p)=\dfrac{\tau}{K\tau_{BF}}(1+\dfrac{1}{\tau p})=A(1+\dfrac{1}{\tau p})\): Régulateur PI mixte
- \(CTM(p)=\dfrac{K(1-e^{-Tp})}{1+\tau p}\): bloc compensateur de temps mort dont nous allons étudier le fonctionnement plus loin.
Pour la démonstration, cliquer ici.
Commentaires:
- Le correcteur de Smith est un correcteur à modèle interne, son algorithme fait intervenir les paramètres du procédé (\(K,T,\tau\)). Pour paramétrer le bloc compenateur de temps mort, il est indispensable de modéliser le système. La qualité de la modélisation influencera grandement les performances de la régulation future.
- Si T=0s, la fonction de transfert du compensateur de temps mort est nul. Le correcteur de Smith se résume à un régulateur PI.
- En entrée du bloc PI, le signal de mesure est corrigé par la sortie du bloc CTM(p) pour aboutir à un signal de mesure corrigé: \(Mc(p)=\dfrac{K}{1+\tau p}Yr(p)\). Le bloc CTM permet de masquer le temps mort naturel du procédé au bloc PI, permettant ainsi d'éviter à l'action intégrale de modifier inutilement le signal de commande entraînant l'instabilité de la boucle de régulation.
Exemple de réalisation:
Ci-dessous la configuration logicielle d'un correcteur de Smith à l'aide du système DeltaV d'Emerson.
A l'aide du bloc DTC (Dead Time Compensator) présent dans la librairie de modules "prêt à l'emploi"
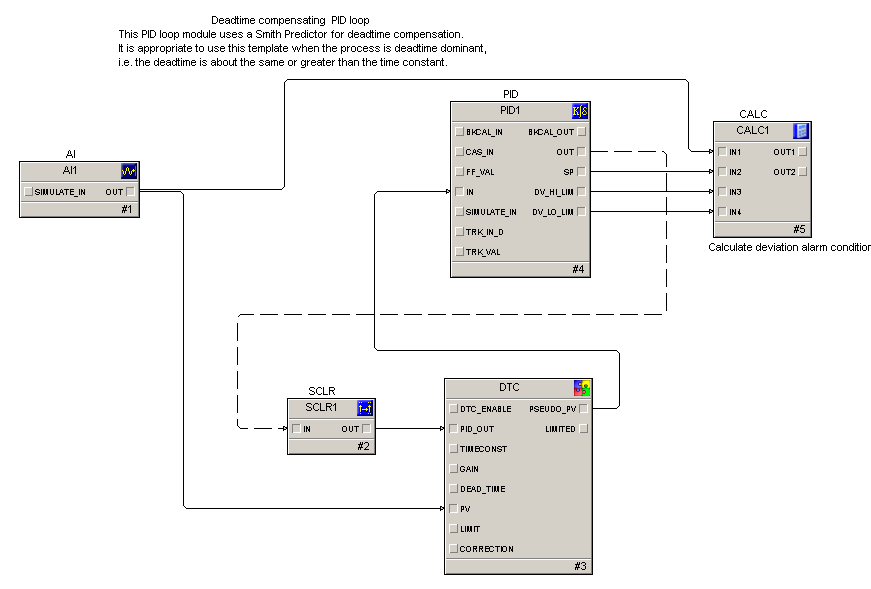
Ou par utilisation d'un bloc temps mort et d'un bloc premier ordre.
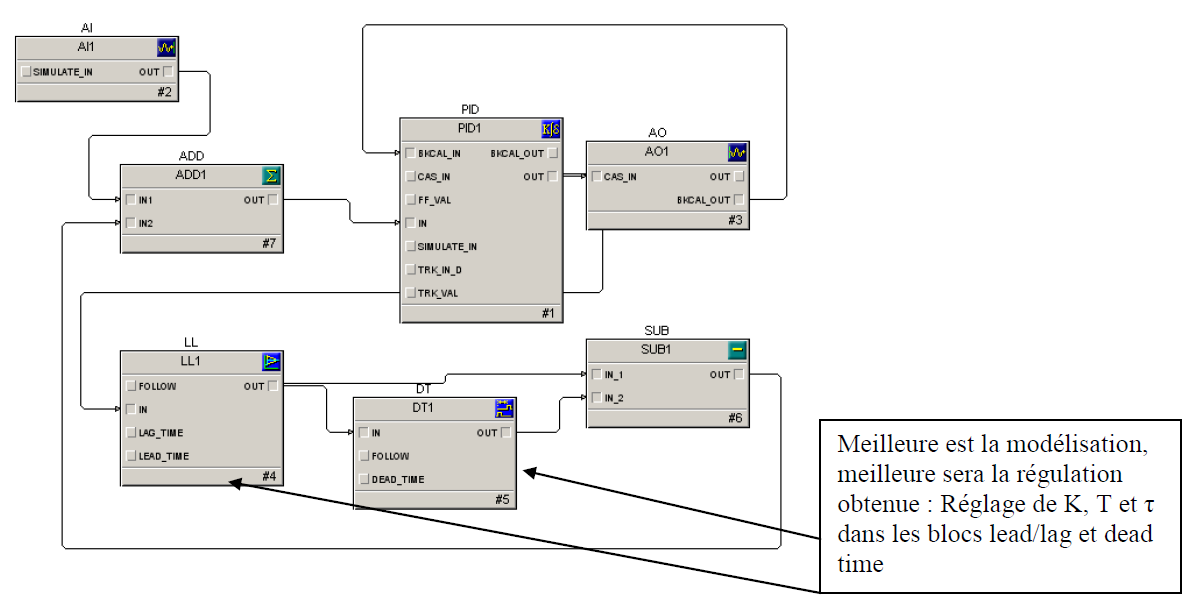
Performances
Reprenons le système du premier ordre retardé \(H(p)=\dfrac{M(p)}{Yr(p)}=\dfrac{Ke^{-Tp}}{1+\tau p}=\dfrac{1.2e^{-3p}}{1+8p}\)
Cette fois ci, il est associé à un correcteur de Smith dont le bloc PI est réglé tel que \(Ti=\tau\) et un gain de boucle \(AK=3\) comme précédemment.
| Avec une modélisation parfaite | Avec un CTM configuré avec \(K_{s}=1.2\),\(\tau_{s}=8\),\(T_{s}=4\). | Avec un CTM configuré avec \(K_{s}=1.2\),\(\tau_{s}=8\),\(T_{s}=2\). |
| On constate que la mesure corrigée est identique au signal de mesure mais varie sans temps mort. | Le moindre écart du modèle mathématique au système réel entraîne une dégradation importante des performances du correcteur de Smith. |